我们在前面讲了线性回归模型，它可以对数据进行预测、拟合。假设有一个二元分类的问题，最终的结果有两类（0,1），此时我们如果使用线性回归模型，那么他的输出结果可能远大于1，或者小于0。这时候我们就需要一个算法使结果的输出一直处于（0，1）之间，这就是我们接下来要讲的逻辑回归算法。它在原有的线性回归算法外面，加上了一个sigmoid函数，使之输出一直处于0,1之间。

Sigmoid函数的公式为：

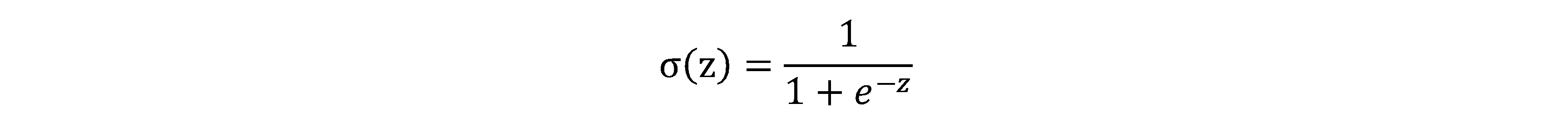
其中z为我们前面所说的线性函数：

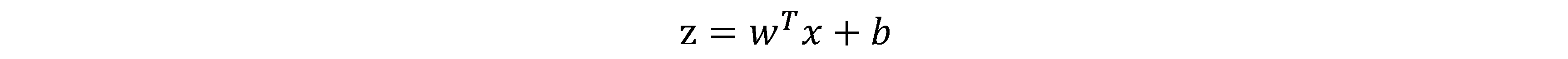
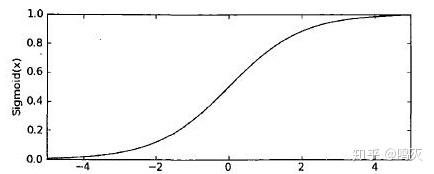
这样最终的预测值就会处于0,1之间，我们将大于0.5的分类为1，小于0.5的分类为0。至于说为什么外面加上sigmiod函数预测值就处于0,1之间，大家可以考虑z，当z特别大时sigmiod函数就会接近1，z非常小时，sigmiod就会非常接近0。下面是sigmiod函数的图像，大家可以自己感受下

损失函数

我们在之前将线性回归的时候讲解了损失函数，但现在我们逻辑回归函数的损失函数与线性回归的损失函数是不同的，线性回归之中用到的损失函数为：

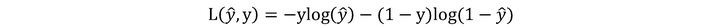
至于说为什么使用这个函数作为逻辑损失函数？大家可以考虑下：

当y=1时，损失函数

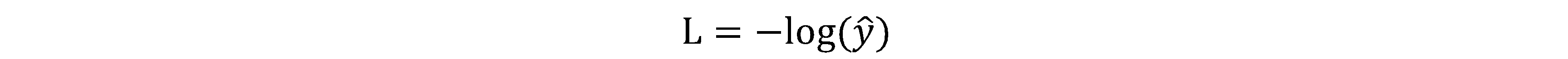
如果想损失函数L尽可能小，那么预测值就要尽可能大，因为sigmiod函数取值[0,1],因此预测值会无限接近1。

当y=0时，损失函数

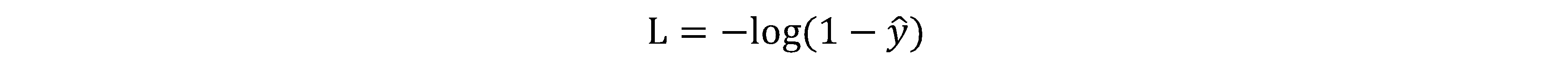
如果想损失函数L尽可能小，那么预测值就要尽可能小，因为sigmiod函数取值[0,1],因此预测值会无限接近0。

参考：吴恩达深度学习视频

下面我们来介绍几种评估模型的几种方法。假设我们目前只有一个数据集D={(x1，y1),( x2，y2),...，( xm,ym)}既要训练，又要测试，该如何去做？

评估方法

1.留出法
将数据集D拆分成为两个互斥的集合，一个作为训练集S，另一个作为测试集D。

需要注意的是训练集与测试集的划分数据尽量保持一致性，可以选择分层抽样的方式，根据比例采样。

另外需要注意的是采用按比例分割仍有多种划分方式，单次使用留出法的得到的评估结果往往不够稳定，因此一般采用若干次随机划分、重复实验的方式取平均值后作为留出法的评估结果。

2.交叉验证法

“交叉验证法”先将数据集D划分成k个大小相似的互斥子集。每个子集 Di都尽可能保持数据分布的一致性，即从D中通过分层采样得到。然后，每次选中k-1个子集作为训练集，剩下的那个子集作为测试集，从而可进行k次训练和测试，最终返回的结果是这k次测试结果的均值。

3.自助法

在留出法与交叉验证法中，由于一部分样本用于测试，因此会造成训练集样本数目过少的情况。在这里我们采用自助法（bootstrapping）作为解决方法。在给定的数据集D中，我们对它进行采样产生数据集 D^’:每次随机从D中挑选一个样本，将拷贝入 D^’中，然后重复m次，这样D中会有一部分样本在D^’ 中多次出现，但仍有一部分样本没有在D^’中出现过。我们将D^’作为训练集，将没有出现过的样本作为测试集。

4.调参

大多数算法都有些参数需要设定，参数配置不同，学得模型的性能的性能往往有显著的差别。因此在模型评估与选择时，除了要对适用学习算法进行选择，还需对算法参数进行设定，这就是通常所说的“调参”。

性能度量

下面说一些性能度量常见的符号。

精确率

召回率

准确率

误分配率

ROC曲线全称是“受试者工作特征”（Receiver Operating Characteristic）曲线。它的横轴为“假正例率”（FPR），纵轴为“真正例率”（TPR），两者分别定义为：

AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。随机挑选一个正样本以及一个负样本，分类器判定正样本的值高于负样本的概率就是 AUC 值。

AUC值越大的分类器，正确率越高。

一、误差

统计学习的目的是是学到的模型不仅对已知数据而且对未知数据都能有很好的预测能力。当我们已经通过训练数据得到模型之后，我们可以用一组新的数据（测试数据）来看看模型效果如何。

我们计算出每个点与模型的距离，然后取平均，计算出平均误差。

我们在训练数据集上得到的误差一般称作“训练误差”（training error），在新的样本上的误差成为“泛化误差”（generalization error）。我们都希望得到一个好的模型可以在新的样本之中得到一个较好的结果，使泛化误差变得更小。

二、过拟合

我们看下面的一张图

图中的第一张表是欠拟合的（高偏差），也就是说它没有很好的模拟出训练集的函数，最后一张表是过拟合的（高方差），因为它过度的拟合了训练集，无法更好的对新的数据进行预测。那么在遇到过拟合的问题时，我们该如何去做呢，一般有两种方式：

1.丢弃一些不能帮助我们正确预测的特征。可以手工标注，或者说使用一些模型来帮忙比如说PCA。

2.正则化。

三、正则化

我们可以看下面的一个公式

我们发现正是由于高次项导致了过拟合问题，如果我们将这些高次项系数接近0，就可以很好的拟合，正则化就是在一定程度上减小这些参数的值。

为了减小这些参数的值，我们需要修改代价函数如下图所示：

我们在代价函数后面给加上θ3、θ4加上了一些惩罚项。因为，如果你在原有代价函数的基础上加上 1000 乘以 θ₃ 这一项 ，那么这个新的代价函数将变得很大，所以，当我们最小化这个新的代价函数时， 我们将使 θ₃ 的值接近于 0，同样 θ₄ 的值也接近于 0，就像我们忽略了这两个值一样。

如果我们不知道那些特征该惩罚那要怎么办呢？我们可以对所有的特征进行惩罚。因此最后的公式变为：

这就是正则化了。

参考：吴恩达机器学习视频

回归问题属于监督学习的一种。它用于预测输入变量和输出变量之间的关系，特别是当输入变量发生变化时，输出变量的值也会发生变化，回归模型正式表示从输入变量到输出变量之间的映射函数。回归问题的学习等价于函数拟合：选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。回归问题分为学习和预测两个过程。下面我们来说一下如何建立这个线性回归模型。

一、模型（Model）

假设我们有一组数据集D={(x1,y1),(x2,y2),...,(xm,ym)}，我们建立了y=b+w*x这样一个函数模型。其中w和b就是这个模型的参数，我们说的调参就是调整这些参数的值。这两个参数可以取任意值，这样我们会得到无穷多的一个函数集，然后我们需要从中选择出效果好的那个函数。

二、损失函数（Loss Function）

我们如何判断函数的效果好与不好呢，这里就需要定义一个损失函数。

F(x_i)的值为我们定义的函数模型预测的结果，Y_i为真实的结果。损失函数也可以展开写成这样：

接下来我们需要使用一种方法解出上面的方程得到参数w,b。

三、梯度下降（Gradient Descent）

我们在这里使用梯度下降的方法来得到参数w与b。

1.首先随机选出一个参数w0,b0

2.计算偏微分

然后不断迭代更新

其中为Learning rate学习率，它决定学习的速度，也就是下降寻找最低点的速度。

3.然后继续计算偏微分

这样不断的迭代更新，直到找到最低点。

我们一般用

来表示梯度下降的过程。

参考：李宏毅机器学习视频，李航统计学习方法。

放假啦，在家里待了几天，所以没更新，接下来恢复更新啦，准备写个机器学习入门的系列笔记，最后感谢各位观看。